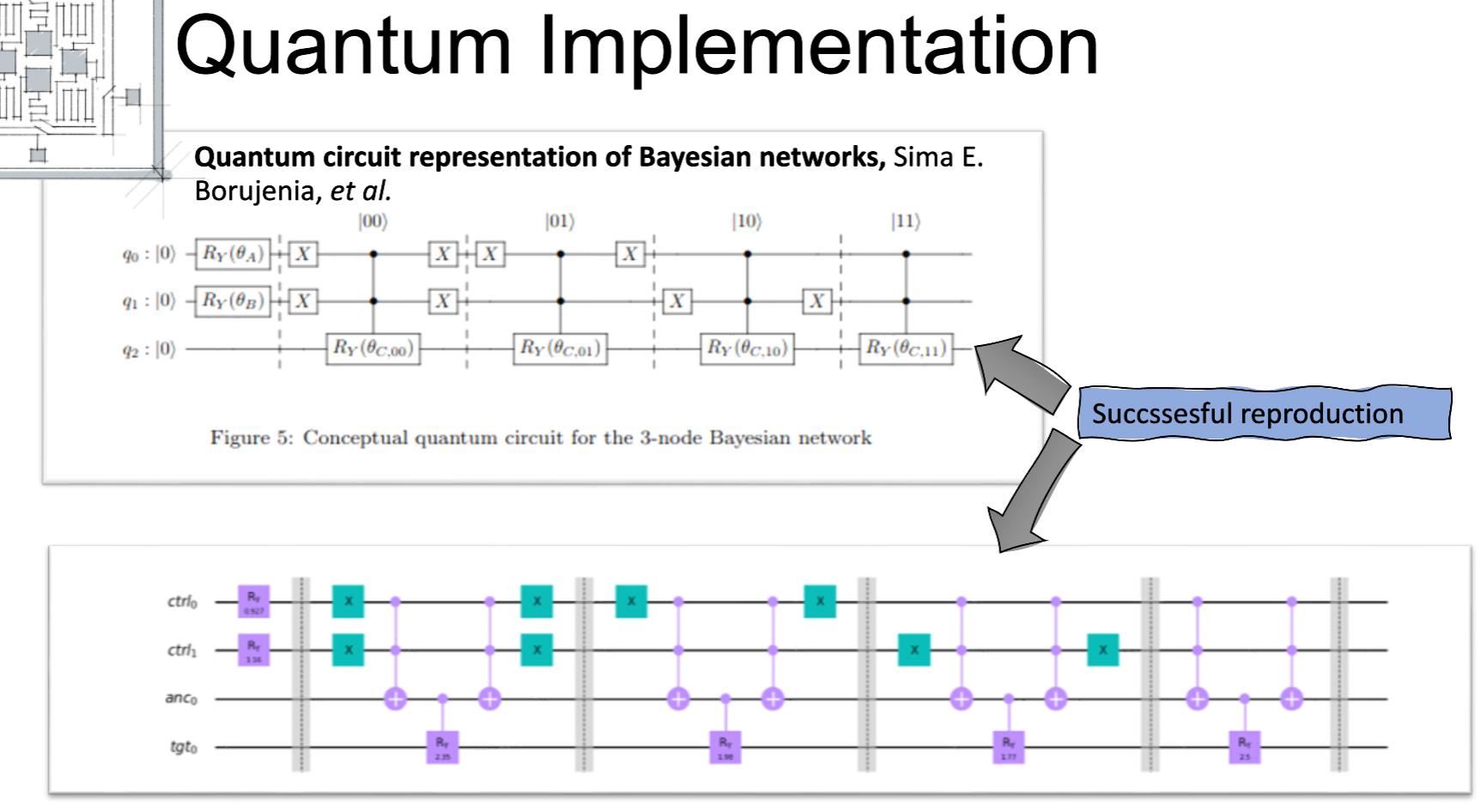
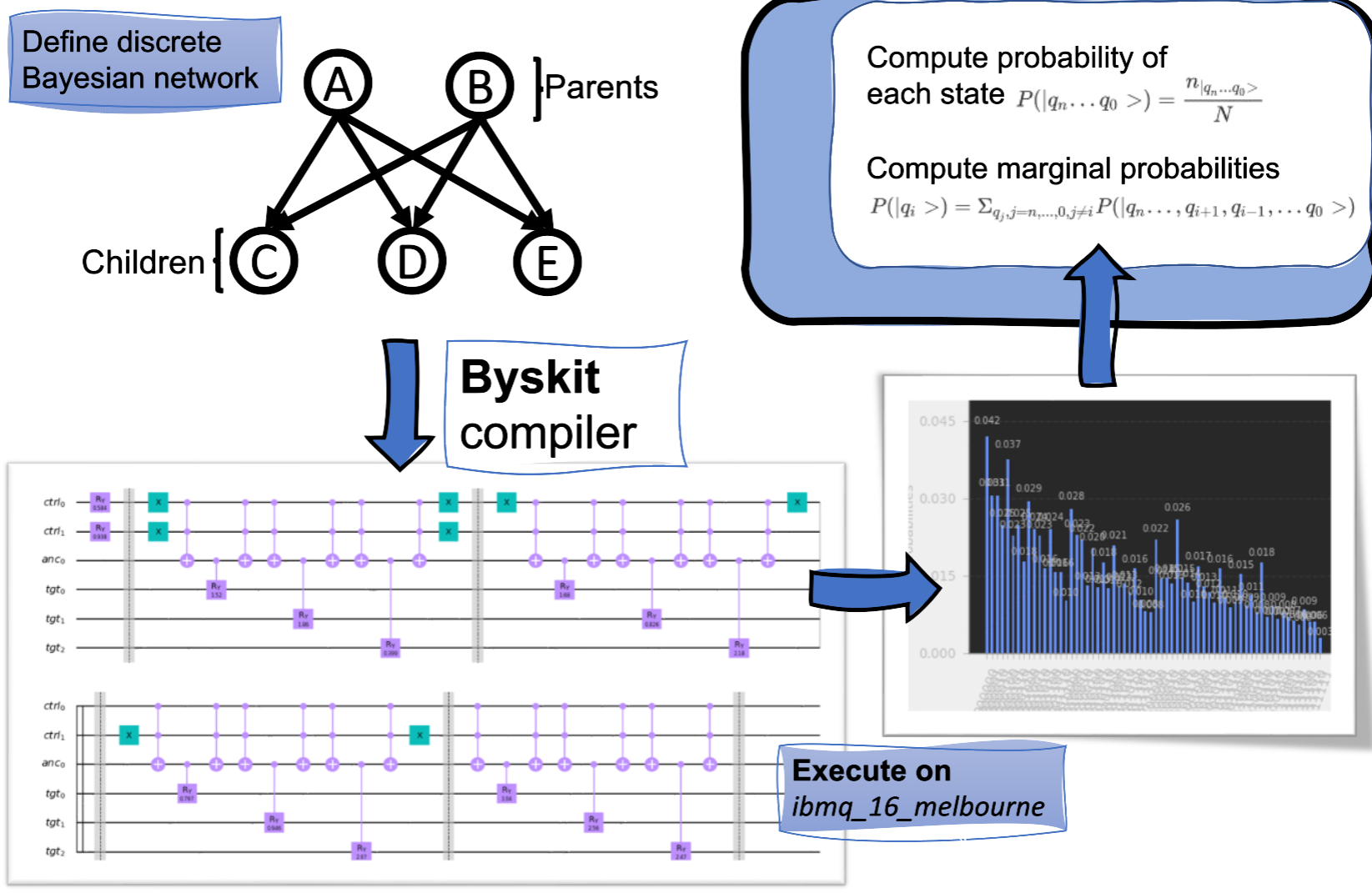
Classical Bayesian Networks.
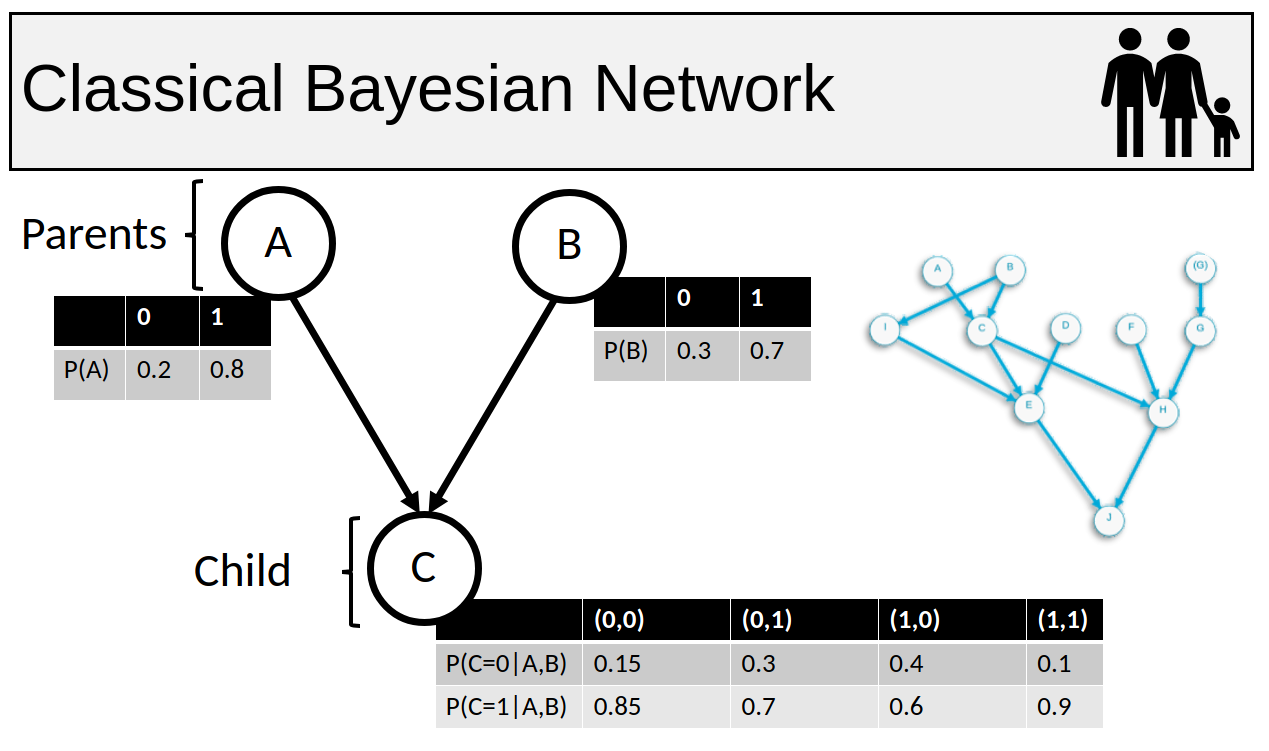
A Bayesian network is a probabilistic model that graphically represents random variables and the conditional dependencies between them. The model is based on a directed acyclic graph with nodes representing random variables and the directed edges between them representing their conditional dependencies. These dependencies are modelled with conditional probability distributions or tables.
These probability distributions can either be specified manually or learned using data. Once they are populated, we can use the network to make inferences of different types. For instance, we can make predictions about outcomes based on a set of inputs, or we can make diagnoses where we infer what inputs may have led to an observed outcome. These inferences can be exact or approximate.
The main graph in this slide is simple, with a child and two roots. However, Bayesian networks can be arbitrarily complex - see the example to the right. Performing exact inference on bayesian networks is sharp-P hard, meaning they become classically intractable as they grow very large. We can use approximate inference to avoid this, but this is still NP hard generally. Approximate inference uses other techniques such as Markov Chain Monte Carlo sampling or rejection sampling methods to speed up inference.