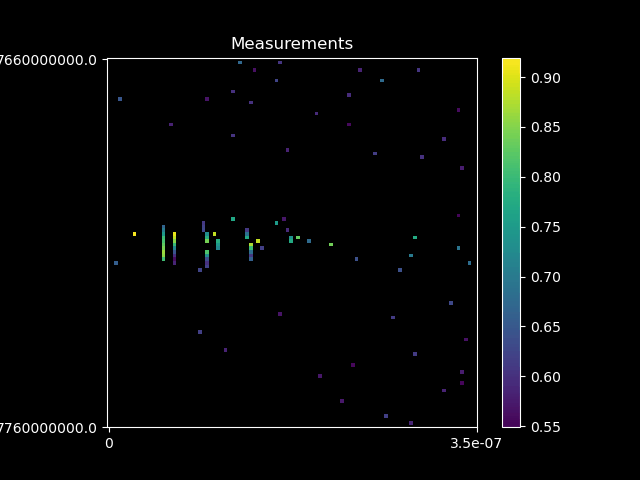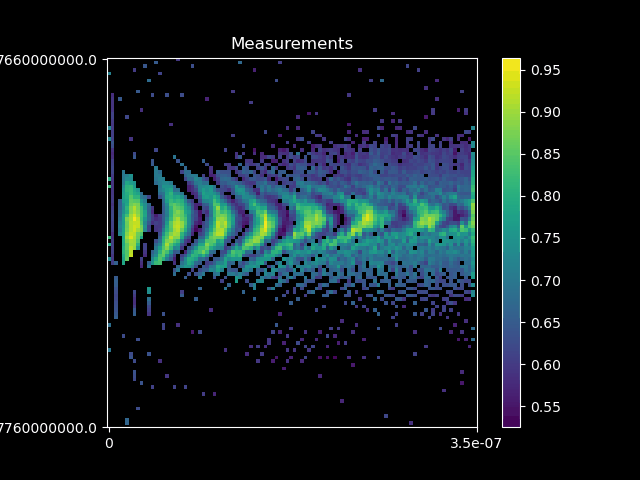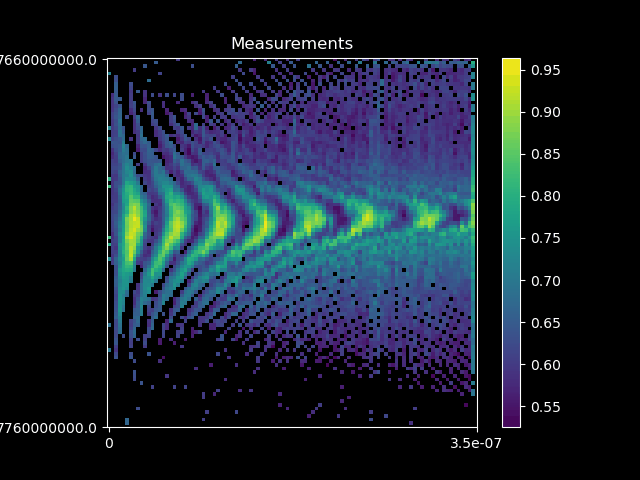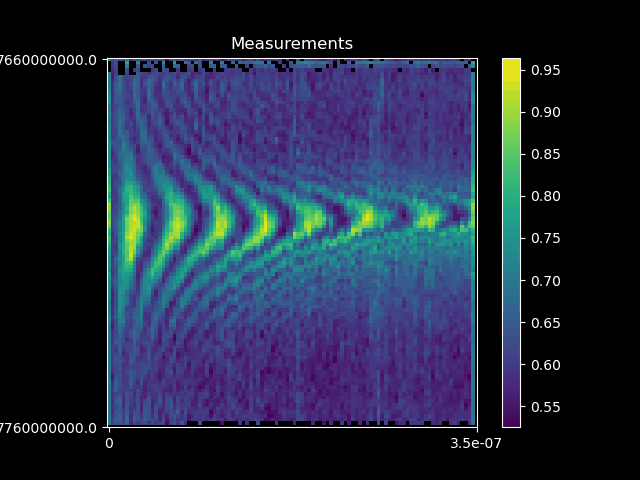
Research - Optimal quantum control.
Optimal quantum control via automatic differentiation.
S. B. Orbell
Quantum gates serve as logical unitary operations on the computational subspace of a quantum system. The fidelity of a quantum gate defines the closeness of the input-output state mapping to that of the ideal unitary operation. It is an essential metric in benchmarking and evaluating quantum devices, as achieving high-fidelity operations is imperative for the practical realization of a fault tolerant platform for running quantum algorithms.
Given a quantum system in a well-defined initial state, and a Hamiltonian describing the dynamics of the evolution of the system under the time-dependent Schrödinger equation
\begin{align}
i\hbar \frac{\partial}{\partial t} \Psi(t) &= \hat{H} \Psi(t) \\
\hat{H} &= \hat{H}_0 + \hat{H}_C [u(t)]
\end{align}
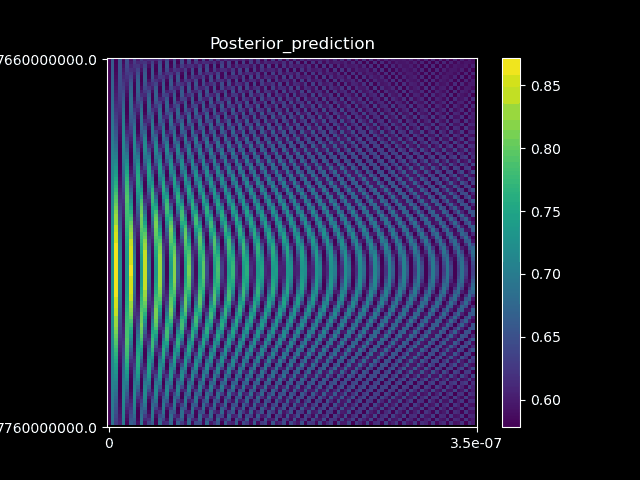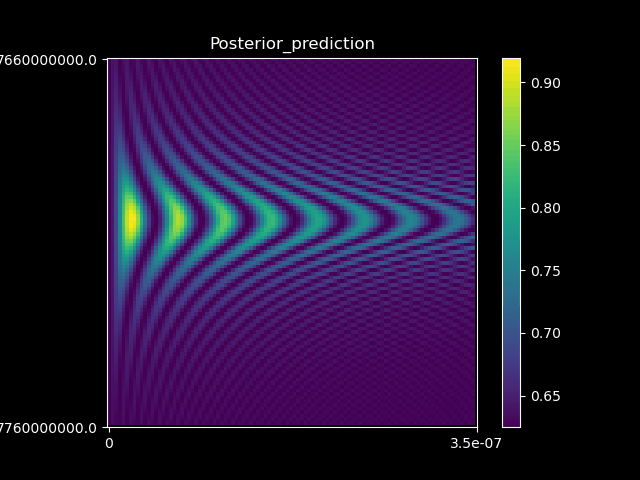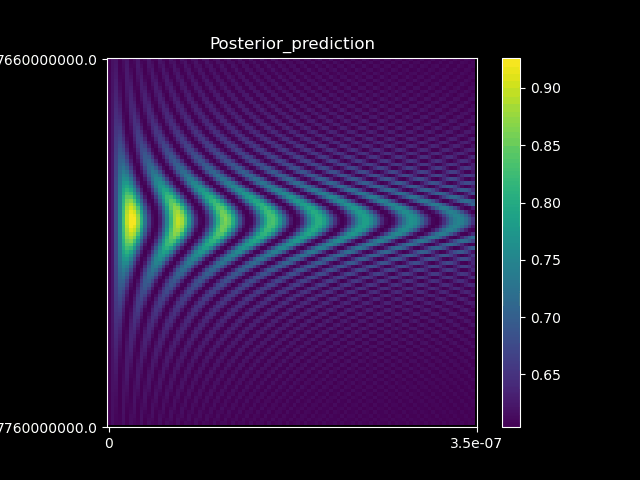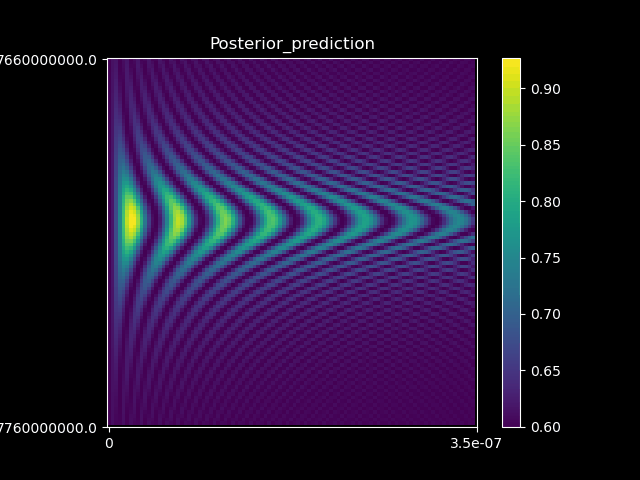
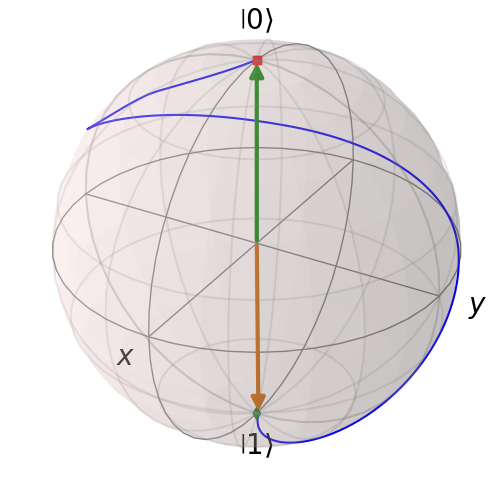
with a drift term \(H_0\) and a control term \(H_C\) defined by a time dependent control vector \(u(t)\). The problem of optimal quantum control is to find a function \(u(t)\) which evolves the system to a desired target state, or implements a target transformation. For a transition to a target state \(\ket{\psi_{target}}\), the solution can be found by minimising the fidelity
\begin{align}
L(u(t)) = 1 - | \braket{\psi_{\mathrm{control}} |\psi_{\mathrm{target}}}|^2
\end{align}
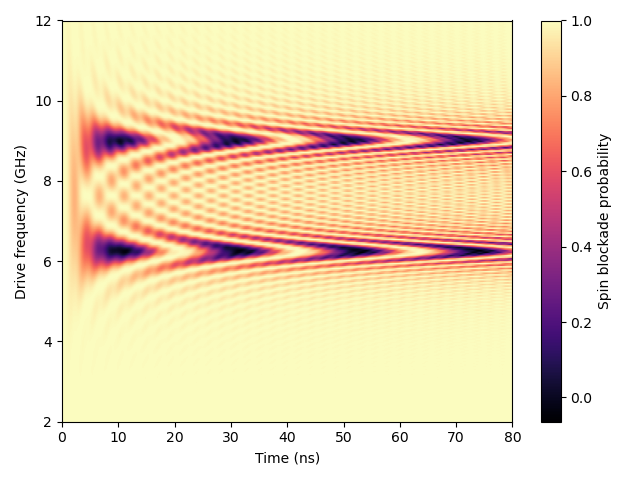
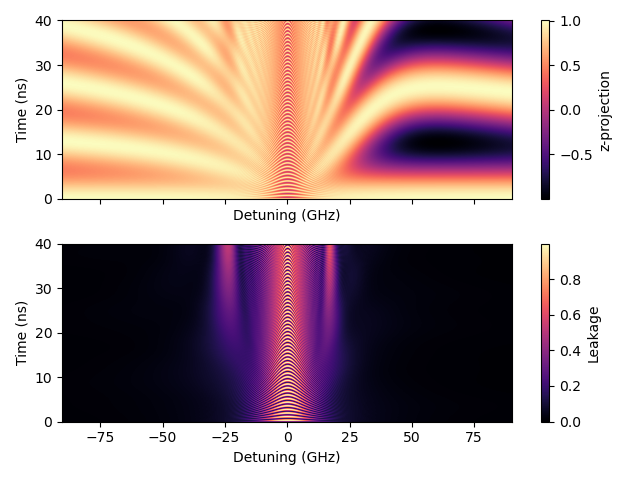
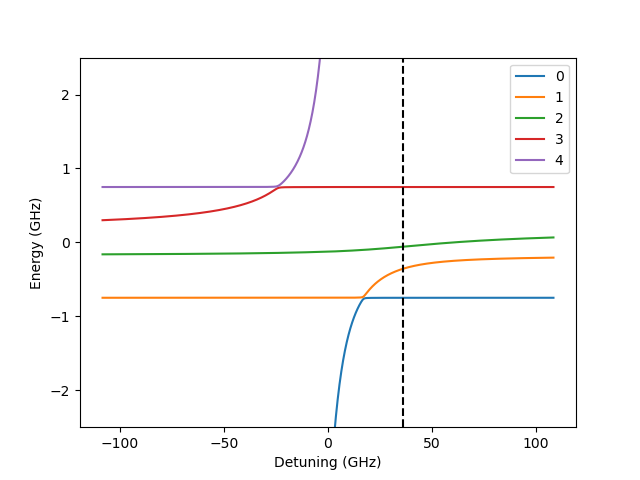
where \(\Psi(t=T) = \ket{\psi_{\mathrm{control}}} = U(u(t))\ket{\psi_{\mathrm{initial}}}\), averaged over a set of initial states, \(\Psi(t=0)=\ket{\psi_{\mathrm{initial}}}\), which define a Haar measure for the system. We use the following Hamiltonian for two-coupled Loss DiVincenzo hole spin qubits at a Si/SiGe double quantum dot.
\begin{align}
H_{eff} = &H_0 + [S, V] \\
H_{eff} = &\left(
\begin{array}{ccccc}
\epsilon & 0 & 0 & 0 & 0 \\
0 &\beta \Sigma & 0 & 0 & 0 \\
0 & 0 & \beta \Delta & 0 & 0 \\
0 & 0 & 0 & -\beta \Delta & 0 \\
0 & 0 & 0 & 0 & -\beta \Sigma \\
\end{array}
\right) + \frac{1}{\epsilon} \left(
\begin{array}{ccccc}
2 \left(t_c^2+t_{\text{SO}}^2\right) & 0 & 0 & 0 & 0 \\
0 & -t_{\text{SO}}^2 & -t_c t_{\text{SO}} & t_c t_{\text{SO}} & t_{\text{SO}}^2 \\
0 & -t_c t_{\text{SO}} & -t_c^2 & t_c^2 & t_c t_{\text{SO}} \\
0 & t_c t_{\text{SO}} & t_c^2 & -t_c^2 & -t_c t_{\text{SO}} \\
0 & t_{\text{SO}}^2 & t_c t_{\text{SO}} & -t_c t_{\text{SO}} & -t_{\text{SO}}^2 \\
\end{array}
\right)
\end{align}
In most cases of interest, an analytical solution to this control problem does not exist, hence optimal control solutions must be found numerically.
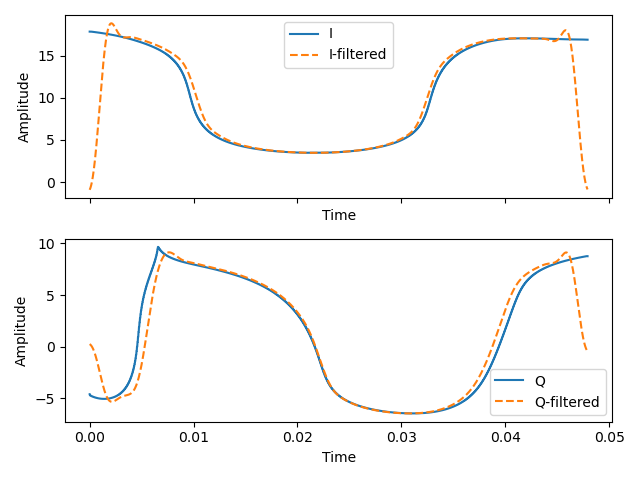
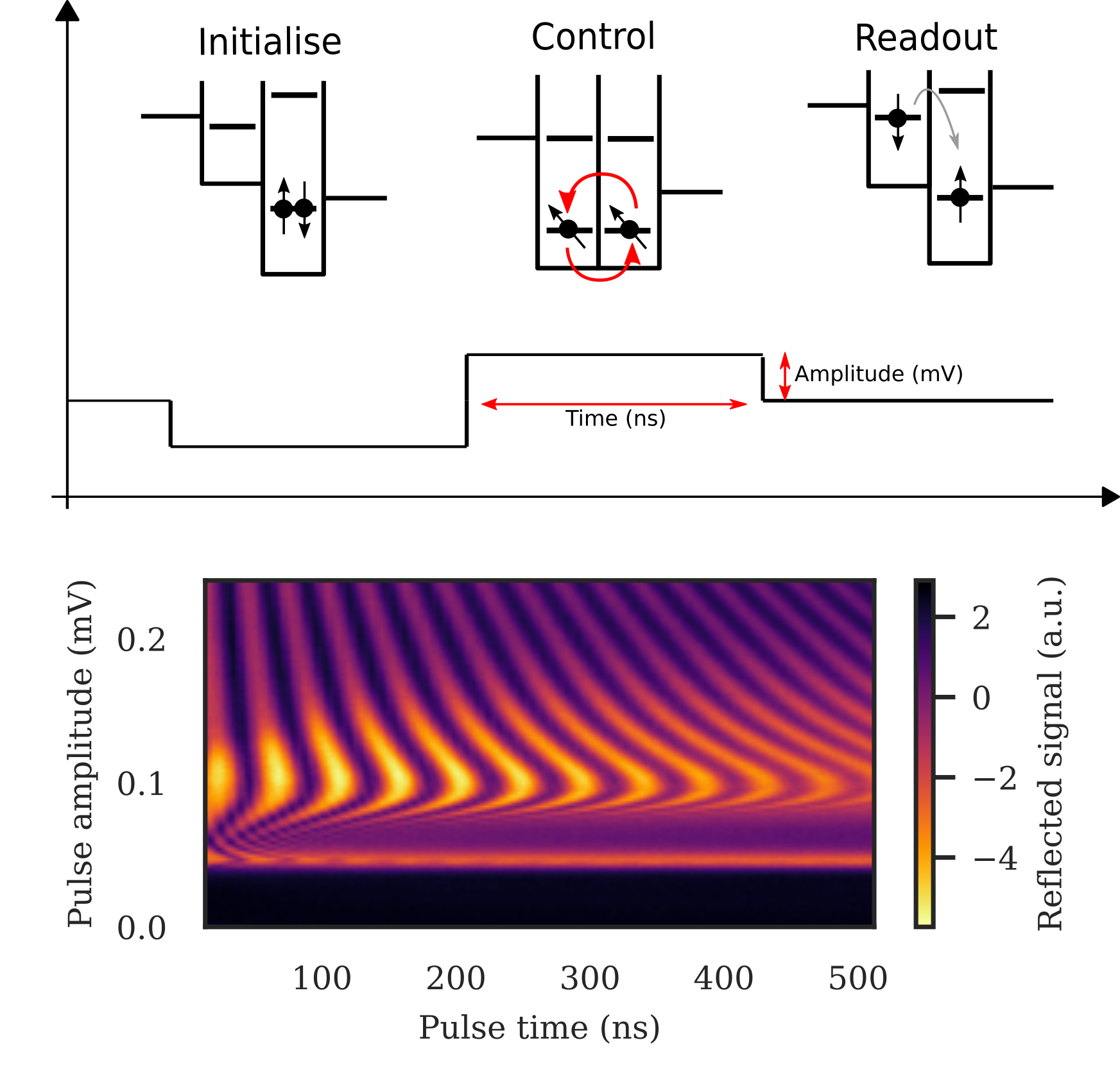
We can optimize the fidelity of quantum operations with respect to the control pulse using a gradient-based optimization technique, namely the ADAM optimizer. The fidelity is computed using time evolution in the Schrödinger picture. This allows for an efficient, iterative refinement of the control pulses, driving the system toward optimal gate operations. The advantage of this method, with respect to previous gradient based optimal control techniques, such as GRAPE, is that we can add any modifications to our simulation, and still trivially acquire gradients. These modifications can include affects from a realistic quantum device measurement setup, such as filtering affects, non-linear transmissions, experimental noise sources.